DE 2 EJEMPLOS DESARROLLADOS PARA USO DE NET LOGO.

 

1.      La figura en los modelos de netlogo es el observador este no está representado en el mundo pero puede interactivo con él.

2.      Se pueden modelar relaciones entre diferentes tortugas mediante links que es el tercer tipo de agente presente en netlogo, los links hacen mediante un par (tortugal, tortugal 2) una relación de las dos tortugas mediante dicho link

¿QUÉ ES NET LOGO Y TIPO DE PROGRAMACIÓN USA?

NetLogo fue diseñado, en el espíritu del lenguaje de programación Logo , estar "bajo umbral y el techo no". It teaches programming concepts using agents in the form of turtles , patches , and the observer . ^{[ 1 ]} NetLogo was designed for multiple audiences in mind, in particular: teaching children in the education community, and for domain experts without a programming background to model related phenomena. ^{[ 2 ]} Enseña los conceptos de programación utilizando agentes en forma de tortugas, parches, y el observador. NetLogo fue diseñado para múltiples audiencias en cuenta, en particular: enseñanza los niños de la comunidad educativa, y por expertos del dominio sin conocimientos de programación con el modelo fenómenos relacionados.

 

 

DE UN EJEMPLO DESARROLLADO DEL MÉTODO DE GRAM SMITH

 

Es un entorno multi-agente de modelos programables. Al ser un entorno de modelado programable nos permite simular fenómenos naturales y sociales. Este es especialmente apropiado para modelar sistemas complejos en desarrollo en el tiempo. Los modeladores pueden dar instrucciones a cientos o miles de "agentes" todos operando independientemente. Esto hace que sea posible explorar la relación entre el comportamiento micro-nivel de los individuos y los patrones de nivel macro que surgen de su interacción.

RESUMA EN QUE CONSISTE EL MÉTODO DE GRAM SMITH

Es método de ortogonalizacion se conoce como el método de Gram-Schmidt, en honor de estos dos matemáticos alemanes que NO inventaron el método, el cual al parecer se le debe al matemático francés P.S. Laplace.

 

El método de ortogonalizacion de Gram–Schmidt permite construir conjuntos en cualquier espacio con producto interno, de dimensión finita o infinita, a partir de una sucesión de vectores no nulos.

 

En este además se nos dice que al poder un conjunto de vectores ortogonales formar una base para un espacio vectorial, es posible construir un conjunto de vectores ortogonales a partir de un conjunto de vectores linealmente independientes.

 

 

 

¿QUÉ ES UN EIGENVECTOR?

Son los vectores no nulos que, cuando son transformados por el operador, dan lugar a un múltiplo escalar de sí mismos, con lo que no cambian su dirección. Este escalar recibe el nombre valor propio, auto valor, valor característico o eigenvalor. A menudo, una transformación queda completamente determinada por sus vectores propios y valores propios.

¿QUÉ ES UNA MATRIZ DIAGONAL?

 

Una matriz diagonal es una matriz cuadrada en que las entradas son todas nulas salvo en la diagonal principal, y éstas pueden ser nulas o no. Toda matriz diagonal es también una matriz simétrica, triangular (superior e inferior) y (si las entradas provienen del cuerpo R o C) normal.

Usos

Las matrices diagonales tienen lugar en muchas áreas del álgebra lineal. Debido a la sencillez de las operaciones con matrices diagonales y el cálculo de su determinante y de sus valores y vectores propios, siempre es deseable representar una matriz dada o transformacion lineal como una matriz diagonal.

De hecho, una matriz dada de n×n es similar a una matriz diagonal si y sólo si tiene n auto vectores linealmente independientes. Tales matrices se dicen diagonizables.

 En el cuerpo de los números reales o complejos existen más propiedades: toda matriz normal es similar a una matriz diagonal (véase teorema espectral) y toda matriz es equivalente a una matriz diagonal con entradas no negativas.

 

 

¿QUÉ ES LA ESTADÍSTICA INFERENCIAL?

La estadística inferencial es una parte de la estadística que comprende los métodos y procedimientos que por medio de la inducción determina propiedades de una población estadística, a partir de una pequeña parte de la misma.

¿PARA QUÉ SIRVE UNA RECTA DE REGRESIÓN?

Determinará la calidad del ajuste. Si r es cercano o igual a 1, el ajuste será bueno y las predicciones realizadas a partir del modelo obtenido serán muy fiables (el modelo obtenido resulta verdaderamente representativo); si r es cercano o igual a 0, se tratará de un ajuste malo en el que las predicciones que se realicen a partir del modelo obtenido no serán fiables (el modelo obtenido no resulta representativo de la realidad). Ambas rectas de regresión se intersecan en un punto llamado centro de gravedad de la distribución.

 

 

¿QUÉ ES UNA RECTA DE REGRESIÓN?

Las rectas de regresión son las rectas que mejor se ajustan a la nube de puntos (o también llamado diagrama de dispersión) generada por una distribución binomial. Matemáticamente, son posibles dos rectas de máximo ajuste.

ECUACION:

 

¿QUÉ ES UN AJUSTE DE REGRESIÓN?

En estadística la regresión lineal o ajuste lineal es un método matemático que modela la relación entre una variable dependiente Y, las variables independientes X_i y un término aleatorio ε.

Este modelo puede ser expresado como:

Y_t=B₀+B₁X₁+B₂X₂+…+B_pX_p+e

 

 

 

¿QUÉ ES JI-CUADRADO?

Es una distribución cuadrática de la probabilidad que utiliza básicamente variables aleatorias continuas. La Distribución Chi Cuadrado de la probabilidad se denota mediante la letra griega minúscula ji elevada al cuadrado (χ²), y consiste en establecer un espacio continuo delimitado por la suma de los cuadrados de n variables aleatorias que son independientes entre sí, espacio dentro del cual la variable X puede asumir cualquiera de los infinitos valores que lo conforman.

Por tanto para establecer el valor aproximado de una variable X dentro de ese espacio se procede a incluir una estimación de sus posibles límites que están dados por los distintos «Grados de Libertad» que pueden existir entre las variables aleatorias analizadas que dan origen al referido espacio.

¿QUÉ ES LA CORRELACIÓN ESTADÍSTICA?

La correlación estadística determina la relación o dependencia que existe entre las dos variables que intervienen en una distribución bidimensional.

 Es decir, determinar si los cambios en una de las variables influyen en los cambios de la otra. En caso de que suceda, diremos que las variables están correlacionadas o que hay correlación entre ellas.

¿QUÉ ES UNA DISPERSIÓN ESTADÍSTICA?

Las medidas de dispersión, también llamadas medidas de variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la mediana media. Cuanto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la mediana media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos.

Para calcular la variabilidad que una distribución tiene respecto de su media, se calcula la media de las desviaciones de las puntuaciones respecto a la media aritmética. Pero la suma de las desviaciones es siempre cero, así que se adoptan dos clases de estrategias para salvar este problema. Una es tomando las desviaciones en valor absoluto (Desviación media) y otra es tomando las desviaciones al cuadrado.

¿QUÉ ES LA VARIANZA ESTADÍSTICA?

La varianza estadística  es la media aritmética del cuadrado de las desviaciones respecto a la media de una distribución estadística.

Esta medida nos permite identificar la diferencia promedio que hay entre cada uno de los valores respecto a su punto central.

Este promedio es calculado, elevando cada una de las diferencias al cuadrado,  (Con el fin de eliminar los signos negativos), y calculando su promedio o media; es decir, sumado todos los cuadrados de las diferencias de cada valor respecto a la media y dividiendo este resultado por el número de observaciones que se tengan.

¿CUÁLES SON LAS MEDIDAS DE TENDENCIA CENTRAL Y ESCRIBA SU DEFINICIÓN DE CADA UNA?

 

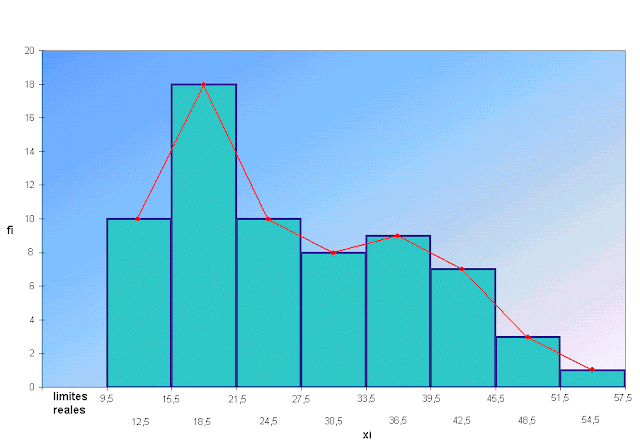
Media:

En matemáticas y estadística una media o promedio es una medida de tendencia central que según la Real Academia Española resulta al efectuar una serie determinada de operaciones con un conjunto de números y que, en determinadas condiciones, puede representar por sí solo a todo el conjunto.

Media ponderada

La media ponderada es una medida de tendencia central, que es apropiada cuando en un conjunto de datos cada uno de ellos tiene una importancia relativa, respecto de los demás datos. Se obtiene del cociente entre la suma de los productos de cada dato por su peso o ponderación y la suma de los pesos.

Media geométrica:

En matemáticas y estadística, la media geométrica de una cantidad arbitraria de números es la raíz enésima del producto de todos los números, es recomendada para datos de progresión geométrica, para promediar razones, interés compuesto y números índices.

Media armónica:

La media armónica, denominada H, de una cantidad finita de números es igual al recíproco, o inverso, de la media aritmética de los recíprocos de dichos valores y es recomendada para promediar velocidades.

Median:

En el ámbito de la estadística, la mediana, representa el valor de la variable de posición central en un conjunto de datos ordenados. De acuerdo con esta definición el conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra.

Moda:

En estadística, la moda es el valor con una mayor frecuencia en una distribución de datos. Hablaremos de una distribución bimodal de los datos adquiridos en una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima.

 

 

 

¿QUÉ SON LAS MEDIDAS DE TENDENCIA CENTRAL?

Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización. Cuando se hace referencia únicamente a la posición de estos parámetros dentro de la distribución, independientemente de que ésta esté más o menos centrada, se habla de estas medidas como medidas de posición.

 

En este caso se incluyen también los cuantiles entre estas medidas. Se debe tener en cuenta que existen variables cualitativas y variables cuantitativas, por lo que las medidas de posición o medidas de tendencia se usan de acuerdo al tipo de variable que se está observando, en este caso se observan variables cuantitativas.

 

INDIQUE 20 COMANDOS BÁSICOS MÁS UTILIZADOS EN MATLAB

 

abs	Valor absoluto
acker	Calcula la matriz K para ubicar los polos de A-BK, vea también place
axis	Corrige la escala del gráfico actual, vea también plot, figure
bode	Dibuja el diagrama de Bode, vea también logspace, margin, nyquist1
c2dm	Pasa del sistema continuo al discreto
clf	Borra la figura (use clg en Matlab 3.5)
conv	Convolución (útil para multiplicar polinomios), vea también deconv
ctrb	Matriz de controlabilidad, vea también obsv
deconv	Deconvolución y división de polinomios, vea también conv
det	Halla el determinante de una matriz
dimpulse	Respuesta al impulso de sistemas lineales de tiempo discreto, vea también dstep
dlqr	Diseño de reguladores LQR lineales cuadráticos para sistemas de tiempo discreto, vea también lqr
dlsim	Simulación de sistemas lineales de tiempo discreto, vea también lsim
dstep	Respuesta al escalón de sistemas lineales de tiempo discreto, vea también stairs
eig	Calcula los autovalores de una matriz
eps	Tolerancia numérica del Matlab
feedback	Conexión de dos sistemas por realimentación.
figura	Crea una nueva figura o redefine la figura actual , vea también subplot, axis
for	Lazo For-Next
format	Formato Numérico (dígitos significativos, exponentes)
function	Para archivos-m del tipo función

¿QUÉ LENGUAJE DE PROGRAMACIÓN USA MATLAB?

EL MATLAB tiene como elemento básico

la matriz, que no requiere dimensionamiento previo y se escribe

tal como se hace matemáticamente, lo cual aporta facilidad yrapidez de uso.

Al ejecutar el programa aparece un indicador de espera para la

introducción de los comandos propios de MATLAB:

 

1. Expresiones.

Se introducen tal como se escriben matemáticamente:

>> a = 4/3 respuesta: a=

1.3333

De esta manera se crea una variable “a” en el entorno de trabajo,

cuyo valor se puede consultar escribiendo su nombre:

>> a respuesta: a=

1.3333

MATLAB reconoce hasta 19 caracteres como nombre de variable

y es sensible a las mayúsculas (a≠A).

Al introducir una expresión sin crear una variable, se genera la

variable ans, que equivale a answer:

>> 4/3 respuesta: ans=

1.3333

 

 

¿QUÉ ES MATLAB?

          Es un software matemático que ofrece un entorno de desarrollo integrado (IDE) con un lenguaje de programación propio lenguaje. Está disponible para las plataformas Unix, Windows y Mac OS X. Entre sus prestaciones básicas se hallan: la manipulación de matrices, la representación de datos y funciones, la implementación de algoritmos, la creación de interfaces de usuario (GUI) y la comunicación con programas en otros lenguajes y con otros dispositivos hardware.

           El paquete MATLAB dispone de dos herramientas adicionales que expanden sus prestaciones, a saber, Simulink y guide. Además, se pueden ampliar las capacidades de toolboxes; y blocksets. Es un software muy usado en universidades y centros de investigación y desarrollo.
    
          En los últimos años ha aumentado el número de prestaciones, como la de programar directamente procesadores digitales de señal o crear codigo VHDL
 

ANGRY BIRDS (FISICA)

Angry Birds Rio Unlock | juegos online gratuito con Games68.com